Fractales – Arquetipos de la creación en la naturaleza, el hombre y la sociedad
Autor: Varios
1. Introducción
 Una hoja de helecho, un copo de nieve, un pulmón o un riñón humano; una nube, la costa de Inglaterra… ¿qué tienen en común? “Fueron hechos perfectos y bellos por el creador de todas las cosas”, diría posiblemente un escolástico medieval. Un matemático moderno dice: “Son fractales”.
Una hoja de helecho, un copo de nieve, un pulmón o un riñón humano; una nube, la costa de Inglaterra… ¿qué tienen en común? “Fueron hechos perfectos y bellos por el creador de todas las cosas”, diría posiblemente un escolástico medieval. Un matemático moderno dice: “Son fractales”.
Los fractales son estructuras geométricas que tienen la propiedad de repetir un mismo elemento geométrico o espacial en cada plano, una y otra vez. Un buen ejemplo de ello, en la naturaleza, es el helecho, cuyas hojas producen copias cada vez más pequeñas de si mismas. Otro ejemplo de fractal lo presentó Apolonio de Perge -discípulo de Euclides, aprox. en el 200 a.C.- creando una figura compuesta de esferas cada vez más pequeñas (imagen arriba).
Los fractales despiertan hoy un interés de carácter variadísimo. Se da entre artistas, periodistas, músicos y científicos. ¿Por qué? Desde luego, no porque los fractales posean -como de hecho es- tanta belleza y aún cuando su estética sea realmente innegable. Y desde luego, tampoco porque los fractales se cuenten entre los conceptos más modernos de la matemática, que tienen aplicación en muchos campos de la vida diaria y la tecnología. Más bien pensamos que los fractales atraen a todos porque reflejan arquetipos universales que se expresan en todos los niveles de la creación. Se los encuentra en la naturaleza, en la evolución del cosmos y en los diferentes campos de la sociedad. En estas estructuras omnipresentes, el hombre también puede reconocerse a sí mismo y ver reflejado su propio camino. Quiera este viaje por el mundo de los fractales hacernos avanzar un paso más en el camino del conocimiento.
Comenzaremos por una explicación matemática que, en caso de una lectura rápida, se podría obviar. Luego seguiremos con la descripción de diferentes facetas de los fractales en la naturaleza, el arte, la música, la literatura y la ciencia, que demuestran la presencia universal de estas estructuras arquetípicas. Finalmente, cerraremos con deducciones filosóficas referentes a las reflexiones fractales en el hombre mismo y lo que se puede aprender de ellas.
2. Aspectos matemáticos de los fractales
Fractales son el concepto general para una clase bastante amplia de objetos geométricos (conjuntos) que tienen la propiedad de ser autosemejantes. Autosemejante significa que, estas estructuras, se componen de copias cada vez más pequeñas de sí mismas. El ejemplo más conocido es la llamada “alfombra de Sierpinski”, que se compone de una copia óctuple de si misma, en factor 3 de reducción. La análoga, en tres dimensiones, es la esponja de Menger, llamada así según el matemático Karl Menger (1902-1985).
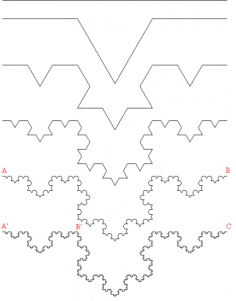
Un conjunto autosemejante también muy conocido es la curva de Koch, con cuya ayuda se puede crear un maravilloso copo de nieve. Este copo de nieve es un fractal, pero no autosemejante en sentido estricto, porque no se compone de copias de si mismo, sino que sólo los bordes se reproducen a sí mismos.
Muchos fractales autosemejantes se construyen “borrando” ciertas partes de un conjunto base (en el caso de la alfombra de Sierpinski, un cuadrado) dentro de una cantidad infinita de repeticiones. Se van borrando partes cada vez más pequeñas, formándose una estructura fractal.
Una construcción alternativa (que lleva el nombre del matemático australiano Michael Barnlsey) se forma reduciendo el tamaño del conjunto base, y luego copiándolo y ordenándolo correctamente (por medio de giros y desplazamientos), repitiendo el proceso infinitamente. Así se forma, por ejemplo, el famoso fractal de la hoja de helecho (primera ilustración).
Un patrón de medida para el “tamaño” de un conjunto fractal y su distribución uniforme es la dimensión autosemejante, que se define como la relación entre el logaritmo natural (ln) de la cantidad de copias del conjunto, en cada paso de la construcción, y el logaritmo del factor de reducción. Así, por ejemplo, la dimensión autosemejante de la alfombra de Sierpinski (8 copias de si misma por paso de construcción, factor de reducción 3) es igual a ln 8 : ln 3 = 1,8927. Este concepto conceptualiza la bien conocida dimensión del espacio. De esta manera, la dimensión de muchos fractales reproducibles en un plano se sitúa entre 1 (dimensión de la línea recta) y 2 (dimensión de un plano).
La palabra fractal fue propuesta en el año 1975 por el padre de la geometría fractal, el matemático polaco de adopción francesa Benoit Mandelbrot. Significa “quebrado, fraccionado, roto” y se refiere, entre otras cosas, a aquella dimensión que a menudo es claramente un número no-entero.
A través de las relaciones numéricas que se dan en los logaritmos (en el caso anterior sería 8:3) los fractales autosemejantes se pueden relacionar con la doctrina de los números y proporciones pitagóricas y, por lo tanto, con la partición de la cuerda (del monocordio), con la doctrina de la armonía musical y de los movimientos de los planetas. Nos podríamos preguntar por ejemplo, qué fractales surgen a través de relaciones numéricas “armónicas” 1:2, 2:3, 3:4, etc. o sea de una relación (musical) de cuarta. De la misma manera, las relaciones de los semiejes de órbitas planetarias en el sistema solar corresponden a proporciones armónicas (doctrina de la armonía cósmica de Johannes Kepler). Con la misma combinación numérica, se puede asociar a fractales la mística pitagórica de los números. Así por ejemplo, el número 3 se puede asignar a la Tríada espiritual, el 4 a la materia y el número 5 al hombre (microcosmos), y con ello llegar a los correspondientes significados para los conjuntos fractales. Simbólicamente, la curva de Koch (y por lo mismo el copo de nieve) podría representar una relación entre los números 3 y 4, o sea entre espíritu y materia, cielo y tierra.
Otra clase importante de fractales son los fractales aleatorios, como por ej. las líneas de un movimiento browniano que representen el movimiento termodinámico caótico de una pequeña partícula en el agua. Tales fractales son conjuntos aleatorios que sólo son “autosemejantes” en un sentido muy irregular. Esto significa que las leyes de la casualidad que los rigen son independientes de la escala y no cambian cuando “aumentamos con el zoom” el conjunto.
3. Autosemejanza en la naturaleza
Los fractales, sean de origen natural o creados matemáticamente, ofrecen un alto grado de autosemejanza. Autosemejanza significa aquí que se repiten formaciones a diferentes niveles de tamaño. Este es el caso por ejemplo, de cuando un objeto se compone de copias reducidas de si mismo (ver por ej. la esponja de Menger o la curva de Koch del punto anterior). Esta propiedad reproduce hasta el infinito en los fractales ideales construidos por cálculo matemático. Al contrario de las formas geométricas, que cuanto más se aumenta la visión más planas y por lo mismo más sencillas aparecen (por ej. una circunferencia), en los fractales aparecen cada vez más detalles y más complejos.
 La autosemejanza en este caso no tiene por qué ser perfecta. En los fractales naturales, la cantidad de niveles autosemejantes de estructuras es limitada y a menudo se sitúa entre 3-5. Ejemplos de esto pueden ser árboles, plantas, nubes, líneas costeras, rocas, arena, copos de nieve e incluso nuestro universo como conjunto, que muestra estructuras fractales de súper-galaxias. Estas formaciones están estructuradas en menor o mayor medida en algunos niveles. Una rama, por ejemplo, tiene más o menos la apariencia de un pequeño árbol. La propiedad de la autosemejanza lleva también a que –por lo menos a determinados niveles aumento- no se pueda decir qué tamaño tenga una sección que estemos contemplando por ejemplo en una foto. El mismo Benoit Mandelbrot habla de la „geometría fractal de la naturaleza“.
La autosemejanza en este caso no tiene por qué ser perfecta. En los fractales naturales, la cantidad de niveles autosemejantes de estructuras es limitada y a menudo se sitúa entre 3-5. Ejemplos de esto pueden ser árboles, plantas, nubes, líneas costeras, rocas, arena, copos de nieve e incluso nuestro universo como conjunto, que muestra estructuras fractales de súper-galaxias. Estas formaciones están estructuradas en menor o mayor medida en algunos niveles. Una rama, por ejemplo, tiene más o menos la apariencia de un pequeño árbol. La propiedad de la autosemejanza lleva también a que –por lo menos a determinados niveles aumento- no se pueda decir qué tamaño tenga una sección que estemos contemplando por ejemplo en una foto. El mismo Benoit Mandelbrot habla de la „geometría fractal de la naturaleza“.
4. Distintas facetas de los fractales
4.1 Arte y arquitectura
Por su dimensión, los fractales están relacionados estrechamente con las proporciones (del arte). Como sabemos, el arquetipo de belleza se expresa entre otras cosas a través de proporciones idóneas. Se pueden encontrar en todos los apartados del arte: en la música con la llamada escala natural (o de tonos concomitantes) y sus intervalos armónicos como la quinta o la cuarta; en monumentos egipcios, estatuas griegas o jardines Zen, todos ellos basados en el número áurico u otras proporciones, por mencionar sólo unos ejemplos.
¿Se puede expresar belleza también fractalmente? Las siguientes imágenes lo demuestran:
Pero ¿se puede hablar de arte si alguien calcula por ordenador una o varias ecuaciones matemáticas y luego aplica un color distinto a cada valor resultante, obteniendo así una imagen fractal? ¿Dónde estaría aquí la creatividad; dónde la fuerza de realización del artista? Los mismos artistas (como ser Jean-Paul Agosti, Edward Berko, Carlos Ginzburg, Jim Long o Susan Conde) se han hecho esta misma pregunta. Su respuesta fue alejarse en parte o totalmente de los ordenadores y dedicarse a pintar con su propia mano imágenes fractales.
También se encuentran fractales en obras de arte de culturas antiguas. Muchos patrones pictóricos de la antigua cultura árabe se nos muestran como notables patrones geométricos fractales (por ej. el techo de la mezquita de Ispahán), o también los dibujos “Kolam” de la India, a manera de mandalas (ver figuras abajo), Estas figuras kolam surgen durante una antiquísima ceremonia que realizan las mujeres de la India cada mañana delante de la puerta de sus casas: sobre el suelo del patio dibujan la llamada Serpiente Kolam para atraer la prosperidad y el éxito.
En un dibujo de Alberto Durero (1520) también se puede ver un fractal. Fue descubierto y descrito matemáticamente en 1915 por el matemático polaco Waclaw Sierpinski.
Todas estas obras de arte fractales tienen algo en común: en ellas domina el orden y el caos al mismo tiempo, como en la misma naturaleza. Esta clase de imágenes viven y se mueven como si algo se estuviera organizando delante de nuestros propios ojos. Como ejemplo valgan las notables imágenes de Jean-Paul Agosti, que contemplan temas mitológicos como el Jardín del Edén y que representan al hombre como puente entre cielo y tierra. Lo consigue a través de fractales que por sí mismos son ya un puente matemático entre lo pequeño y lo grande, entre lo finito y lo infinito, entre la unidad y la multiplicidad y entre lo simple (la igualdad) y la complejidad (la aparición de las formas). Temas eternos que se expresan con métodos modernos.
4.2 Música
¿Como puede ser fractal la música? Y si es así, ¿cómo suena? La primera pregunta es fácil de responder afirmativamente: las frases musicales pueden ser autosemejantes cuando se repite la misma estructura en tono más grave o más agudo en determinados desplazamientos de tiempo. Una composición con esta característica se puede considerar fractal. Desde los años 70 se están realizando experimentos en este sentido. Conocidos músicos que trabajan en ello son: Bernard Fort, Hugh McDowell, Chris Sansom, Gödric Wilkie y, quizás el más conocido de ellos, Richard V. Voss, que trabaja con la repetición de estructuras en 1/frecuencia. Sin embargo, todos estos experimentos han terminado hasta ahora en una música más bien poco estética. Para la ciencia moderna sigue siendo un enigma el por qué sucede esto con los fractales acústicos, al contrario de con los visuales.
Curiosamente, algunos investigadores se siguen preguntando si ciertas piezas de Bach, con sus contrapuntos, no tengan algo de fractal en si mismas, porque en estas obras se repite un motivo una y otra vez con un cierto desplazamiento.
4.3 Literatura
La idea de la autosemejanza se ha abordado también en la literatura. Algunos autores de novelas o poesías repiten con frecuencia un patrón de descripción determinado. J. Swift, por ejemplo, escribe: „Sobre los hombros del naturalista hay una pulga que, sobre su lomo, lleva una pulga más pequeña, que lleva una pulga aún más pequeña sobre su lomo, que…”.
En el último tiempo han surgido también novelas fractales. Incluso en Internet se encuentran textos bajo los términos de búsqueda: novela ó historia fractal.
4.4 Ciencia y tecnología
Una de las tareas de la ciencia es describir el mundo material o mensurable para comprenderlo mejor. En los datos resultantes se basa entonces la tecnología moderna. Se ha demostrado que los conceptos fractales describen algunos complejos sistemas, y su evolución o desarrollo, mucho mejor que otros modelos. Por eso actualmente hay ingenieros que utilizan modelos fractales para, por ejemplo, proyectar materiales de construcción porosos, es decir con espacios huecos, de mejores propiedades. Se ha llegado a la conclusión de que una pared porosa con una estructura y distribución fractal de los espacios huecos amortigua el sonido de manera más efectiva que una pared con huecos repartidos regularmente sobre la misma superficie. Se sabe igualmente, que las costas amortiguan las violentas olas del océano mucho mejor cuando tienen una forma irregular que si fueran relativamente rectas. Se demostró que la erosión de una costa se estabiliza cuando tiene una estructura fractal con una dimensión de 4:3. Cuando la dimensión de la costa es otra, el grado de erosión es claramente más alto.
La idea de que, en la naturaleza, muchas estructuras ideales son fractales, ha inspirado a científicos a buscar soluciones óptimas para la tecnología. La amortiguación del ruido, arriba mencionada, es un ejemplo de ello. Otro ejemplo más sería la distribución óptima del calor en un sistema de calefacción. Se consigue a través de una estructura y geometría fractal del sistema de tuberías.
Los fractales se han impuesto también en muchos otros campos donde se dan procesos relativamente caóticos. Ayudan a calcular –mejor- lo imprevisible. Así por ejemplo, hoy se aplican modelos fractales matemáticos en la economía financiera, para predecir la evolución de la cotización bursátil con “cierta probabilidad”.
5. Filosofía de los fractales
- Como es arriba, así es abajo. Como lo grande, así lo pequeño
El concepto moderno de la autosemejanza refleja la sabiduría antigua de las leyes herméticas bajo una nueva forma. El conjunto de esas leyes (conocidas como la Tabla Esmeraldina) se atribuye al antiguo dios greco-egipcio de la sabiduría y las ciencias Thot-Hermes Trismegisto (el maestro tres veces grande).
Su segunda ley dice en latín:
“Quod est inferius, est sicut id quod est superius, et quod est superius, est sicut id quod est inferius, ad perpetranda miracula rei unius”.
La traducción aforística sería: “Como es arriba, así es abajo, y como abajo, así es arriba. Así en lo grande como en lo pequeño”.
Este principio de las correspondencias o analogías significa que la idea central de un ser se repite en diversos planos y de manera muy parecida. Lo vemos por ejemplo en la estructura septenaria del cosmos, que se refleja en la estructura septenaria del hombre, y ésta a su vez en la estructura septenaria de cada cuerpo, y después en los subcuerpos… etc. Lo esencial se hace presente en todos los planos una y otra vez, y lo podemos descubrir en todos ellos. La autosemejanza es un aspecto científico de ese principio de la correspondencia.
La comparación de la autosemejanza entre los fractales naturales y los matemáticos nos enseña algo también: la autosemejanza en lo mental (es decir, en un fractal creado matemáticamente) es perfecta. Estructuras parecidas se repiten hasta en lo más pequeño. Y así también es el parecido del hombre (lo Pequeño) con el cosmos (lo Grande). Pero si contemplamos la realidad de lo material, entonces la autosemejanza es limitada en algunos niveles y no perfecta, tal y como lo vemos en los fractales naturales del mundo formal. El hombre formal es entonces sólo un reflejo imperfecto de la creación cósmica y lo divino. Para llegar a ser perfecto tenemos que elevarnos a lo puramente mental, en sentido amplio, a lo espiritual.
- Puente entre planos inmortales del Ser
Tal y como Benoit Mandelbrot reconoció, la denominación de fractal fue una elección desacertada, ya que el concepto viene del latín “fractum”: “quebrado, roto en partes, fraccionado” y, por consecuencia, da la impresión de una unidad desgajada. Los fractales sin embargo, hablan simplemente de complejidad, de unidad en la multiplicidad. No separan, sino que unen mundos que, para algunos filósofos, parecían inconexos, como ser: micro- y macro-cosmos, materia y espíritu, lo uno y lo múltiple, lo finito y lo infinito.
- Arquetipos del crecimiento y de la evolución
Los fractales son arquetipos de la evolución que penetran tanto el micro como el macrocosmos. Su efecto se manifiesta en diversos planos de la realidad: en la naturaleza, en el cosmos y en la sociedad, como se ha descrito en varios ejemplos de este artículo. El crecimiento utiliza patrones fractales. En el seno de viejas estructuras se forman nuevas, que corresponden en esencia a las antiguas pero que también contienen una adaptación a las circunstancias actualizadas. Son las mismas de siempre, adaptadas al nuevo ambiente. Estas nuevas estructuras redundarán a su tiempo en impulsos de nacimiento de otras estructuras.
Esta forma de la evolución no se da, ni con mucho, sólo en lo físico. A menudo, se dan también en la psique humana, en la que, por ejemplo, se reproducen patrones que el hombre repite continuamente variando la forma y a diferentes planos. Tales patrones pueden estar ya marcados (astrológicamente) desde el nacimiento o bien desarrollarse a lo largo de la vida. Pueden ser tan fuertes que llegan a influenciar significativamente muchas decisiones y actuaciones en la vida, muchas veces de manera inconsciente.
Así es que, y de esta manera, se pueden formular patrones positivos en la conquista de nuevos territorios psíquicos, mentales ó espirituales en pocos conceptos filosóficos, a saber: valor para el cambio, fidelidad a si mismo, no apegarse al pasado, entusiasmo místico, alegría, entrega…
El alma, como fractal en si mismo, guarda posibilidades ilimitadas de renovarse cada día. Podemos nacer de nosotros mismos todos los días de nuevo. Y en cada día, en cada acción, se esconden todas las facetas del hombre. En cada momento se puede conocer toda la verdad. En cada acción se puede descubrir lo divino, lo esencial del hombre. Si este proceso natural se ve impedido, surge el estancamiento, que entonces puede llevar a problemas psíquicos como los miedos, complejos o incluso enfermedades psíquicas. Todos conocemos el hecho de que casi todas las células del cuerpo humano se renuevan regularmente. Sin embargo, la importancia de un tal proceso para la psique le es desconocida a muchas personas. Deberíamos aprender a ver el mundo con nuevos ojos en cada momento, con los ojos de la Afrodita de Oro (la eterna juventud del concepto griego), para liberarnos de clichés adquiridos, del peso de opiniones “absorbidas” y para entrar en contacto con el Dios en nosotros.
La ciencia moderna ha reconocido que la visión mecánica determinista del mundo, como la tuvo Newton, no corresponde a la realidad y que la “casualidad” juega un papel esencial en nuestro mundo. Los fractales son instrumentos matemáticos de la ciencia moderna que dejan más espacio al caos y a lo imprevisible. Los fractales, por lo tanto, representan un puente entre caos y orden, de manera que allí donde reina el caos hay un lugar para el orden, y viceversa. Esto significa que orden y caos son dos fuerzas inseparables y esenciales de la naturaleza, y que, inalienablemente, hay fases de orden y fases de caos. El cosmos respira, como el antiguo dios Brahma del mito de la creación hindú, y esa respiración se hace sentir hasta en lo microscópico.
En este aspecto, los fractales aleatorios, o casuales, reflejan un patrón combinado de casualidad y orden. Nos dan la idea de que en cada estructura hay un lugar para el orden igual que también es necesario un espacio para la casualidad. Tanto si se trata de pequeños como de grandes ciclos de la historia de la humanidad, o como si se habla de la vida de un sólo ser: todo sigue la ley de la unidad inseparable de orden y caos. Esta ley nos enseña que, incluso un plan perfecto tiene que dejar espacio para la improvisación y las sorpresas, y que para la auto-organización de la naturaleza hay que dejar abierta una cierta inestabilidad del orden. Esto es aplicable también a grupos de personas, los cuales deberían de ser conducidos dejando siempre un espacio libre para la individualidad. El arquetipo de los fractales casuales da una respuesta a la eterna pregunta que el hombre se hace sobre el destino y la libertad, o sobre la combinación de predeterminación y casualidad, en la vida humana. La respuesta es sencilla: ¡la vida se compone de ambas!
6. Epílogo
Nuestro viaje por el mundo de los fractales llega aquí a su fin. Hemos visto lo universal de estos arquetipos en la creación. Se encuentran en la naturaleza, en el hombre y en la sociedad. Los fractales tienen pues su justo lugar en el reino de las ideas. Estos arquetipos son eternos e inmutables mientras que el universo siga existiendo, por lo menos en su forma actual. Su significado llega a todos los hombres y lo entienden todos, cada uno a su nivel e independientemente de su situación o estado social, nivel de educación o intelecto. Se reflejan en todos los planos del universo y de la cultura humana. Son arquetipos de crecimiento y evolución, del juego entre el micro y el macrocosmos, entre orden y caos.
Y de la misma manera en que un cielo estrellado en una noche clara, maravilla a un viajero nocturno, así quiera la belleza de un fractal elevarnos e inspirarnos ideas de eternidad.
Bibliografía
Fuentes generales
-
- Tangente, Hors série N°18 : La magie des fractales
- Bernard Sapoval: Universalités et fractales, 1997.
- GEO, Wissen : Chaos und Kreativität, Nov. 1993
- Fuentes matemáticas
- K. Falconer. Fractal geometry. Mathematical foundations and applications. 2nd ed, Wiley, 2003.
- K. Falconer. Techniques in fractal geometry. Wiley, 1997.
- B. Mandelbrot Die fraktale Geometrie der Natur. Basel, 1991.
- H.-O. Peitgen, H. Jürgens, D. Saupe. Chaos and fractals. New frontiers of science. 2nd ed., Springer, 2004.
- H. Zeitler, D. Pagon. Fraktale Geometrie – eine Einführung. Vieweg, 2000.
- Fractales en el arte
- S. Condé, Ed. L’art fractal. La Différence, 2000.
- S. Condé, Ed. Fractalis, la complexité fractale dans l’art. La Différence en 1993.
- Die Kolam-Figuren Südindiens, Spektrum der Wissenschaft 6 / 2003, S.74.
- Fractales en la música
- M. Gardner. Fractal music, hypercards and more. Freeman, 1992.
- A. Zalmanski. Les scintillements de Richard Voss, Artikel der französischen Zeitschrift „Tangente“, pp. 50-51 (Hors série N° 18: La magie des fractales)
- WWW-Links
- http://www.fraktalroman.de/main02.htm
- http://www.lactamme.polytechnique.fr
- www.f-lohmueller.de/links/indexfrd.htm
Créditos de las imágenes: Blog ecologista, Geometría fractal, Miguel Raban, Fernando S. Aldado, L'officiel des spectacles
Si alguna de las imágenes usadas en este artículo están en violación de un derecho de autor, por favor póngase en contacto con nosotros.





el universo refractario que seria entonces.———
Excelente es un enorme paso en la evolución humana ,en el conocimiento de la geometría sagrada del cosmos y del caos ,en la esencia del alma del pensamiento consciente hacia ka energía universal
Increíblemente poético y completo. La Naturaleza como guía de Evolución,
geometría, I Ching, simbolismo, una clase de psicología práctica y matemática… todo en un mismo y sintético artículo.
Me encantó!
Muy iluminador! Me aclaro de inmediato mis dudas y confusiones sobre el destino, el libre albedrio y el karma.